Project 3

In this third project we create an algorithm which will seamlessly transition from one image to another, or even more! This will involve implementing a correspondence program in order to divide our source images into triangular regions.

Part 1. Defining Correspondences

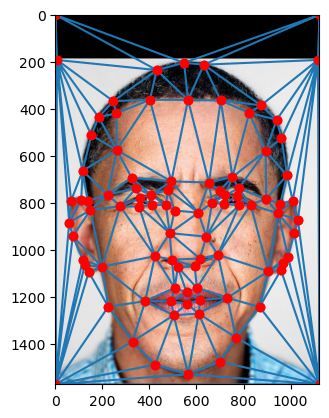
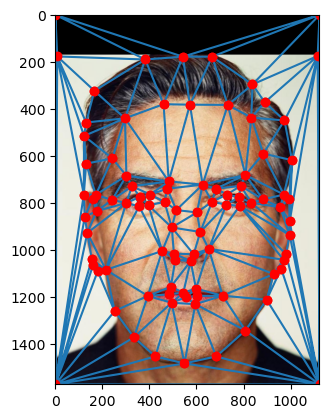
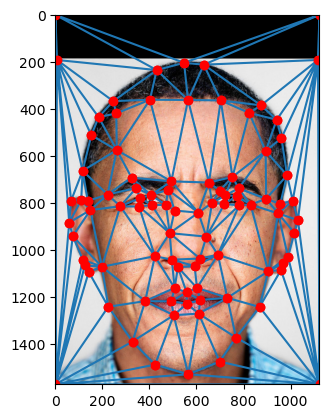
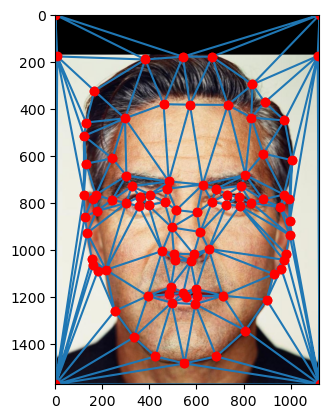
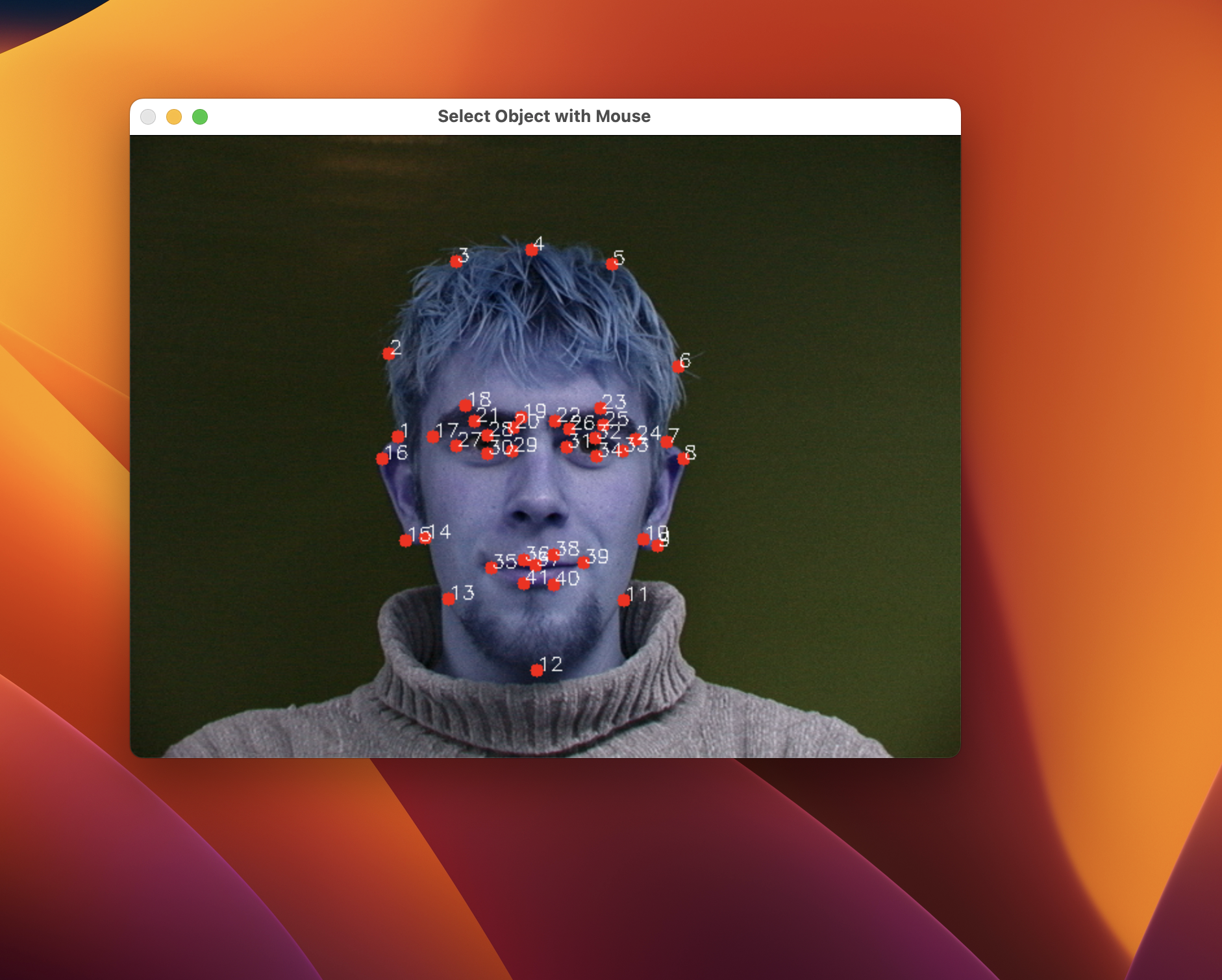
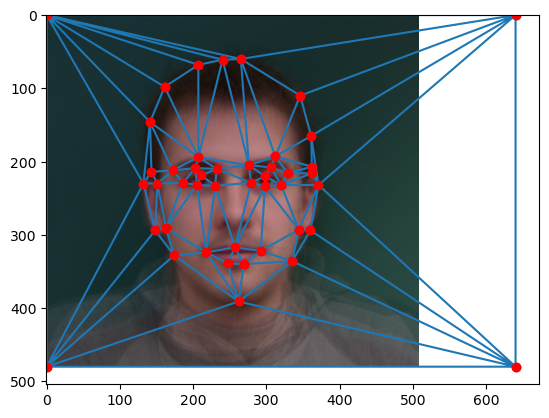
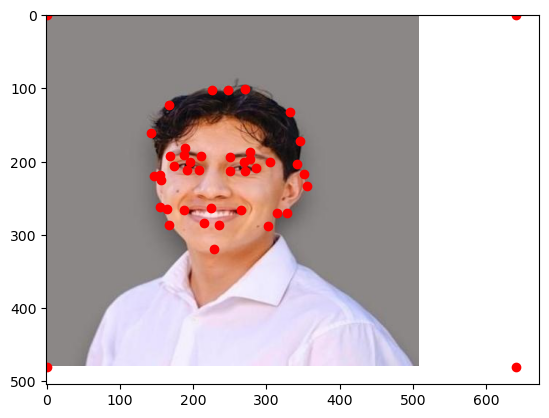
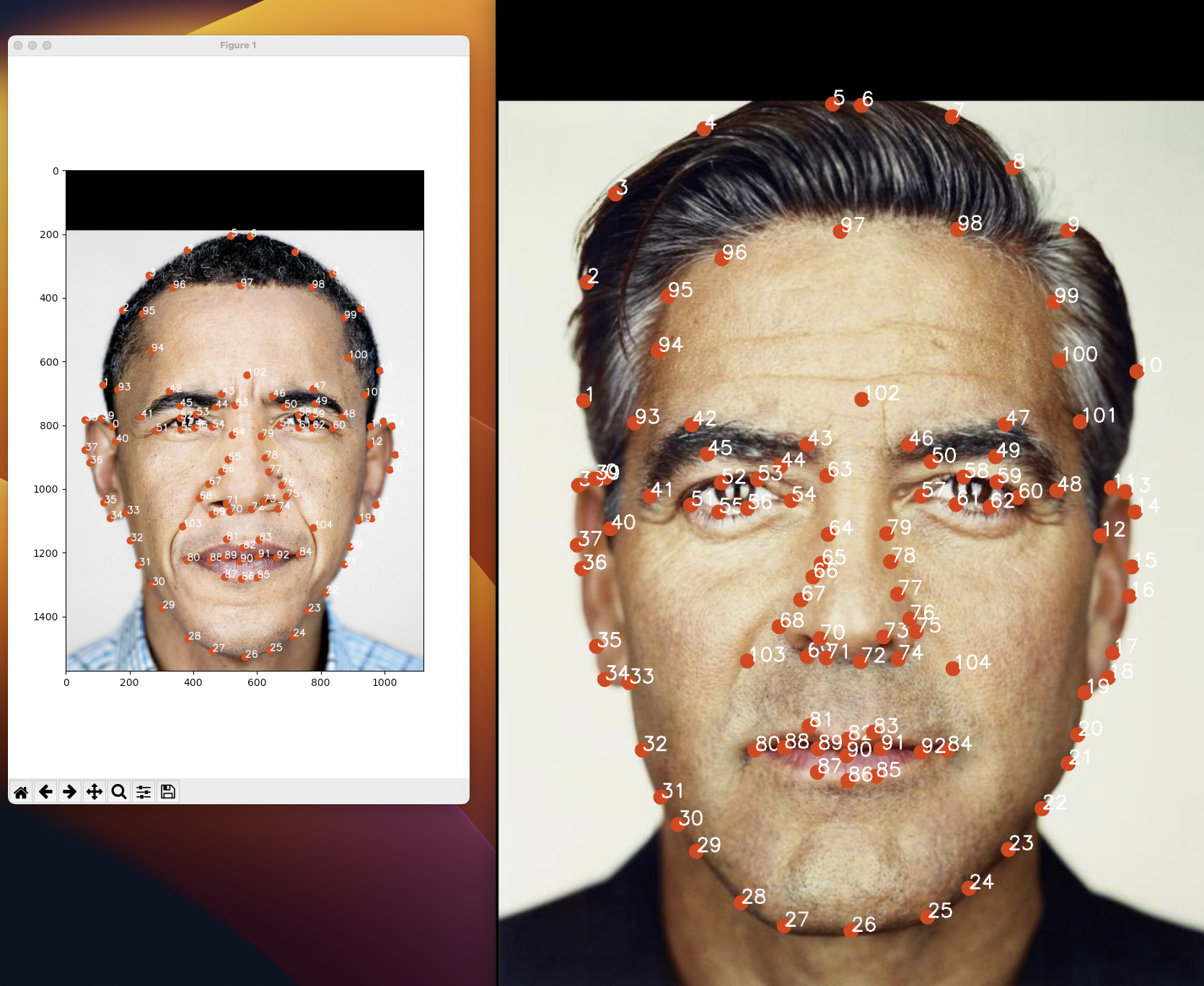
In order to create a linear map or affine transformation from one image to another, we need to find reference points. It will take a really long time to do this for each pixel or super small polygons, so we opt for triangles created by Delaunay Triangularization! Below is a program which I made to define correspondences, the reference points or “anchor” points of each image which we will map with bijective polygons! First, we choose points

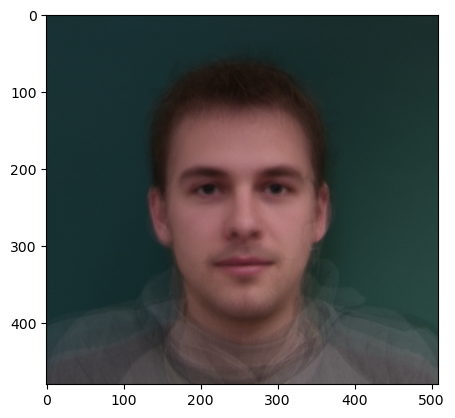
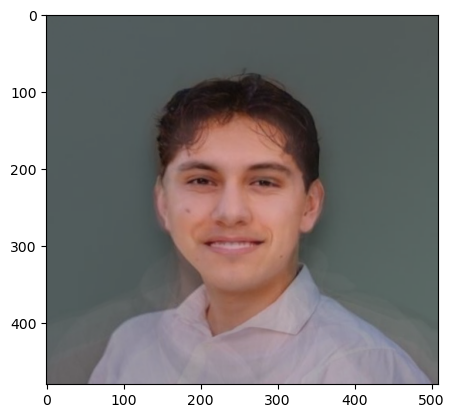
Part 2. Creating the Midway Face

In order to create a midway face of two images, in this case Obama and George Clooney, we must use the correspondences to create triangular meshes. Next, we compute the affine transformation for each image’s triangles into the mean points, which is the simple interpolation of the Delaunay coordinates, which are then

Behold, Georbama: (Two different sets of correspondences)

Part 3. Creating the Morph Sequence

By linearly changing the morph_frac and dissolve_frac of our morphed images, we can create a smooth transition accross both images. Morph_phrac controls how much to weight the average between the two sets of weights and disdolve_frac controls weighted average of the pixels from each morphed image. The result is a 3D tensor of frames which gives us a smooth gif!

Boomerang GIF of Obama and George Cooleny

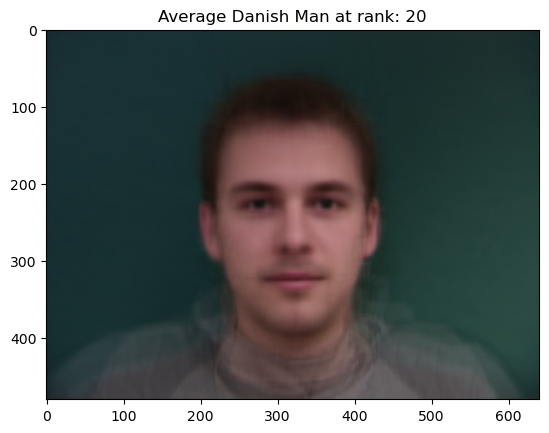
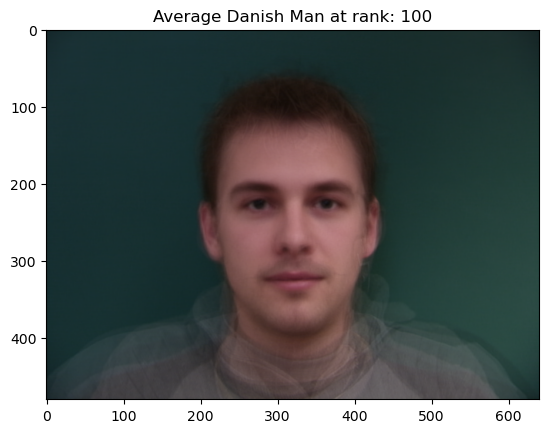
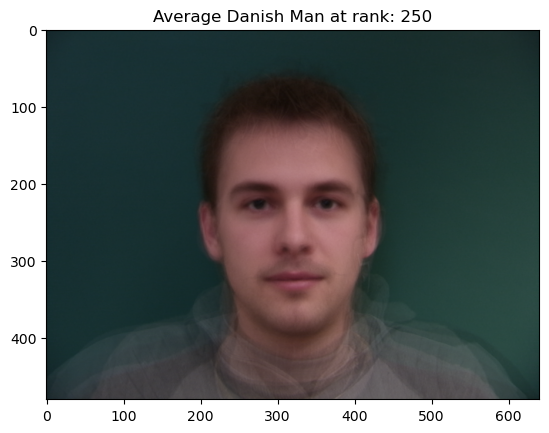
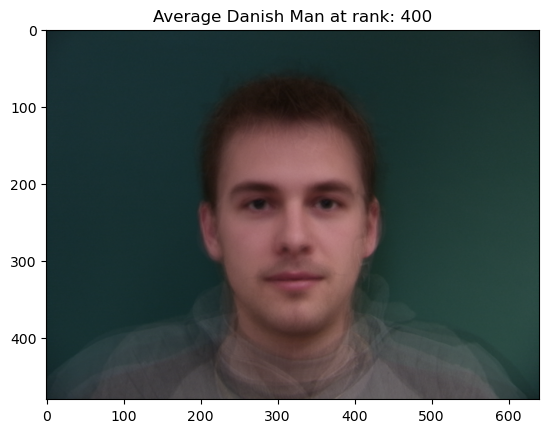
Part 4: The “Mean Face” of a Population ( + Bells and Whistles PCA Basis!)

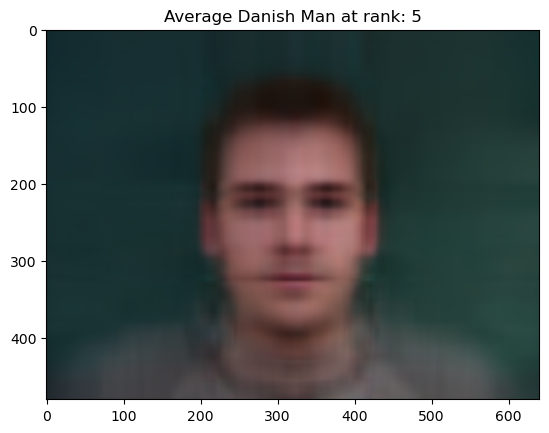
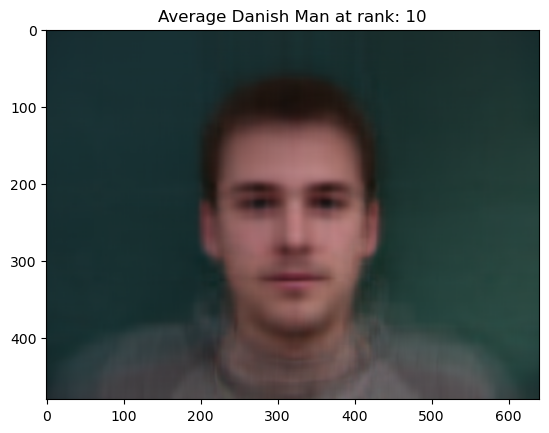
Next, we can cleverly find the “Mean” face of population by morphing samples to fit the mean shape of the Correspondences for each sample. In other words, we morph samples to fit the average “template” and then sum out and average over the morphed images. As a result, we get a better layout of information. However, we’re not done yet. Unfortunately, each image has noise which gives us a highly perturbed average! In order to fix this we extract the most information from each image by taking low-rank approximations, allowing us to control the amount of noise in each image. The resulting mean looks a lot like a real person instead of a blurry or highly perturbed image.

PCA “Averages” which we use later for smoother morphing of “caricatures”

Sample Images from morphs:

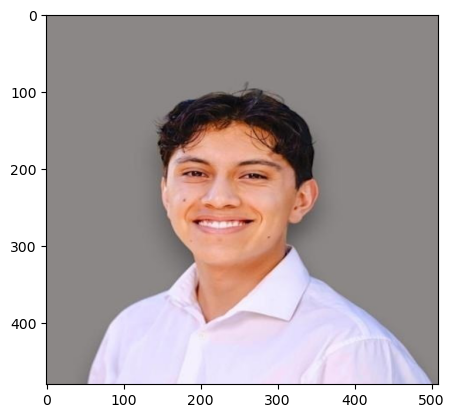
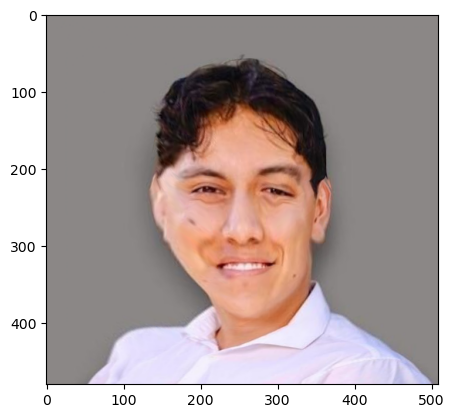
Part 5: Caricatures: Extrapolating from the Mean

Using the previous mean image, we can map a face (mine) to the shape of the mean face, while preserving the color and polygons of my face. To do this, we create
First, we morph without dissolving, then we try finding a mean image by dissolving the mean pixels into my face pixels.

Warping to Mean with no Dissolve

Bells and Whistles: Morphing with a PCA image

Using the PCA basis allows us to get rid of a lot of the outliers and unique features which stray from the mean image. The result allows us to create beter looking morphs that blend a lot smoother.

Bells and Whistles: Morph Classmates

Video compiled by Camille Dang and Steven Luo.

Order:
David(Me) -> steven -> david -> steven -> clara -> steven -> clara -> camille -> clara -> camille -> clara -> steven -> clara -> steven -> david -> steven -> david

URL: https://youtu.be/OgBwQ1yH06E