Introduction

By finding homographies between objects in images, we can find a map which allows us to form mosaics, imaging what it would be like to have a greater field of view. Since humans can see wider a lot of cameras, capturing panoramic images through mosaics can visualize the human vision and beyond!

Shoot the Pictures

Shot by me. I went to UC Riverside for a conference and took pictures of the empty study room across the hallway from the main meeting room.

Everything except these house images were taken by me. Found online: (This was taken from this dataset)

Recover the Homographies

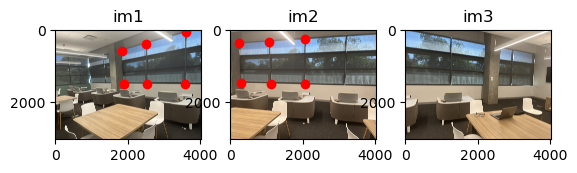
By finding the homography between two images, we find matrix H such that Hp = p’,or equivalently:

We can solve for the values of the matrix by creating a system of equations with 8 degrees of freedom as such:

Because the solution to the system does not always exist, we attempt to find the best solution through least squares. In addition, the use of least squares enables us to solve an over-determined system, possibly leading to more robust measurements of the homography if done correctly, otherwise this can introduce noise to the linear problem.

Warp the Images

Image Rectification

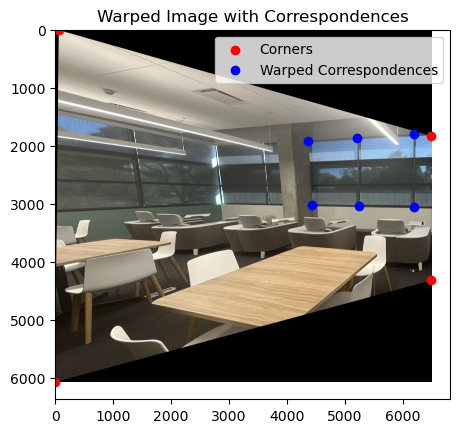
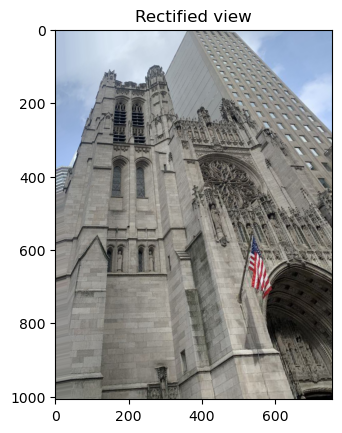
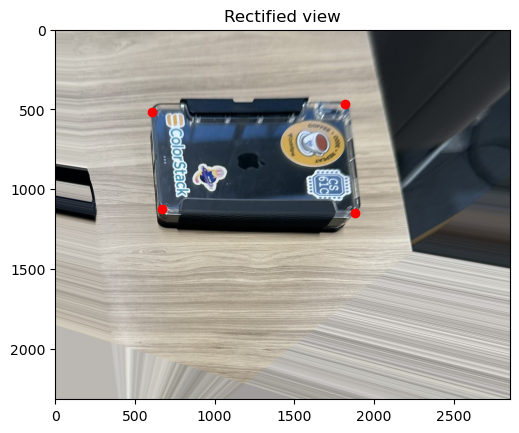
By finding the homography from a warped shape to it’s direct orthographic view, we can estimate the correspondence points of the correct view. This can lead to a lot of variance because this must be inferred, so with some trial and error, a visually-pleasing result can be made.

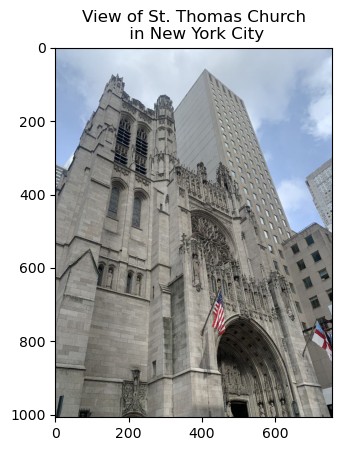
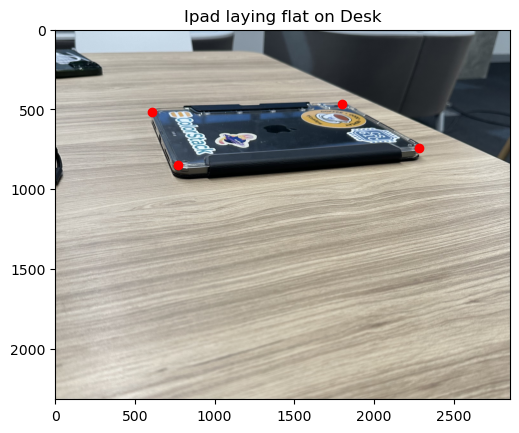
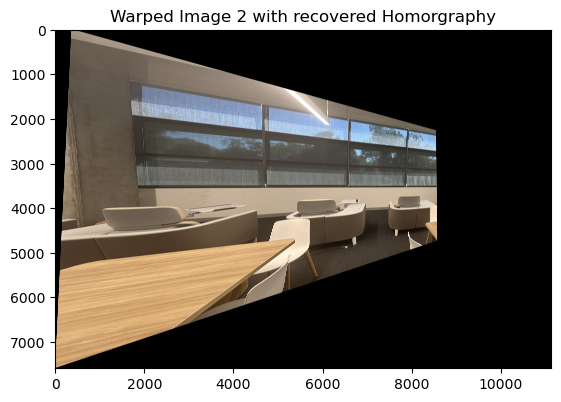
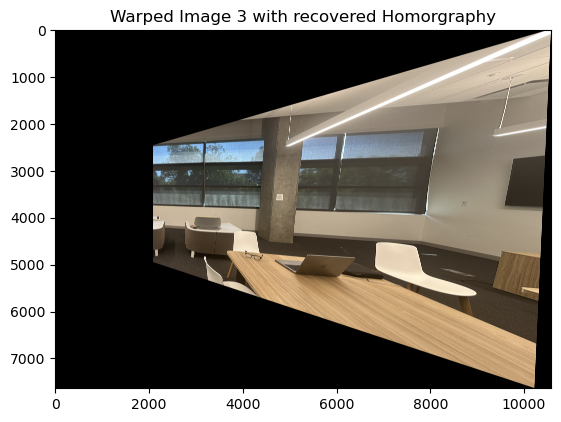
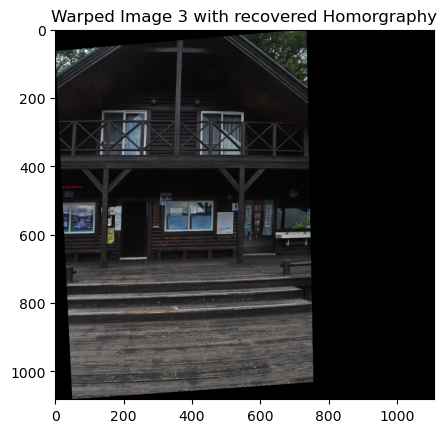
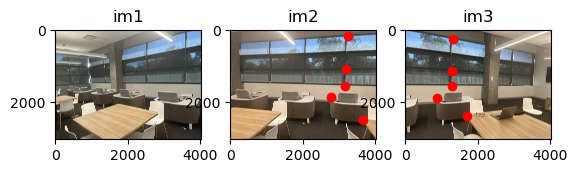
With these sets of correspondences we can solve for the homography and apply it to the entire image. (Pictures shot by myself. Travelled to NYC in September, captured a picture of the mural at MoMA in SF, and took a picture of my iPad with it’s numerous stickers.

Blend the Images into a Mosaic

By finding homographies between objects in images, we can find a map which allows us to form mosaics, imaging what it would be like to have a greater field of view. Since humans can see wider a lot of cameras, capturing panoramic images through mosaics can visualize the human vision and beyond!

After warping by the homography to the target image, the polygon must be shifted into the positive domain or recentered if it is not in the correct domain through a translational transformation. This can be computed by taking the minimum of each dimension of the corner coordinates, and shifting appropriately. We have two ways of aligning the images after one has been warped: 1. We can use the shift vector that we computed in the warping; However, this can be a bit off if we do not account for image sizing and padding correctly. Instead, I found a more stable approach in which I take the mean of each set of correspondences to create two interpolated points. The distance I shift by is the signed distance between the mean points. (Found through subtraction)

Function WarpImageWithPadding(image, homographyMatrix):
    Create coordinate grid for original image
    Transform image corners using homography matrix
    Calculate required padding to fit warped image
    Create new canvas of appropriate size
    Find polygon of warped image area
    Map source coordinates to destination using inverse homography
    For each color channel:
        Interpolate pixel values from source to destination
    Return warped image, shift vector, and transformed corners

For blending, I opted for a combination of Distance-based and Gaussian-based blending which blends two images by creating smooth transitions at their edges using distance-based weights and Gaussian blurring. The result is an image which fades smoothly.

Function BlendImages(image1, image2, mask1, mask2):
    Convert masks to float type
    Calculate distance from edges for both masks
    Compute normalized weights based on distances 
    Smooth weights using Gaussian blur
    Expand weights to match image channels
    Multiply each image by corresponding weights and add together
    Clip result to valid pixel range
    Return blended image

Mosaic 1

Mosaic 2

Mosaic 3

Mosaic 6

By creating the halves, we could then create new correspondences and combine the 2 mosaics to create a larger mosaic!

Mosaic 5 (Example of Bad Correspondences)

In these images of the house, we see that the position of the camera’s perspective point was changed, so we get artifacts when creating the reconstruction. In the first set of images, I made sure to keep the perspective point constant. As a result, those images were smoother and had lines which lined up correctly. In this example, even though the poster is lined up correctly, the stairs and roof are totally off. This is indicative of a bad transformation from inconsistent imaging parameters. As these images of the house were not captured by me, I will have to work with what I can. To improve the map, I can tradeoff accuracy on the poster for overall image improvement. This can be solved with an overdetermined system and least squares, which I employed in previous parts! In mosaic 6, we see this improvement.

Mosaic 6

By carefully selecting points and adding blending, we can create the a better looking. This involved finding parts of the image which captured the homography more clearly. Parts of the image which could have been affected by wind or objects in the way were not as reliable, so using more points led to a more robust measurement. In a way, this is described by the law of large numers, by adding more points we get closed to the true mean homography!

Project 4B

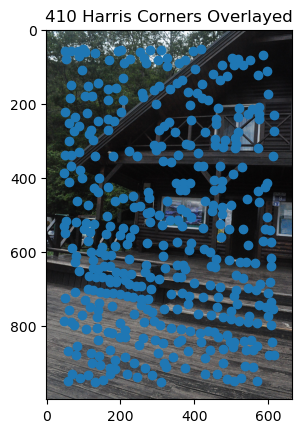
Steps 1: Harris Corners

The paper

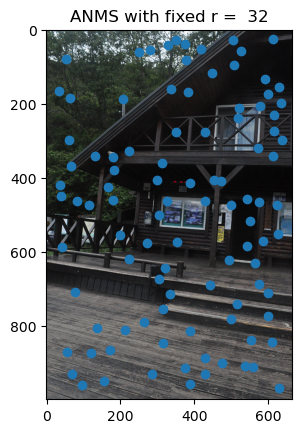
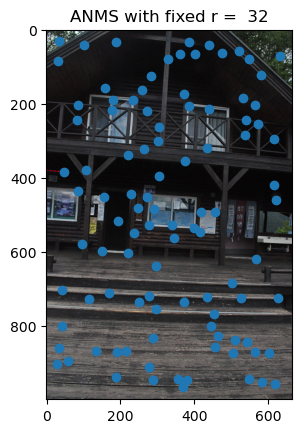
Step 2: ANMS

We can also set a fixed r value and use the adaptive algorithm to generate points of interest which avoid small, tightly packed corners such as those in trees!

With lower radius settings, ANMS yields preserves a lot of the tightly-packed Harris Points. However, increasing the radius allows us to “prune” more of those small and misleading corners which would could mislead the nearest neighbors algorithm in the next steps.

Samples Used at r = 32:

In the two images below. We see that some of the feature points match across the images. In particular, these corresponding points are the corners of windows and the door frame. In addition, some points on the stairs and railing match. However, the most promising points are the door frame and windows, which I used in part 4A when we had to manually assign correspondence points for the homographies.

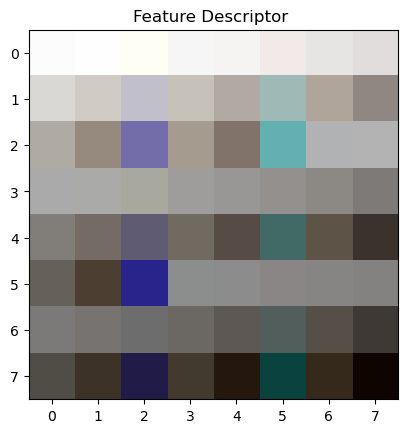
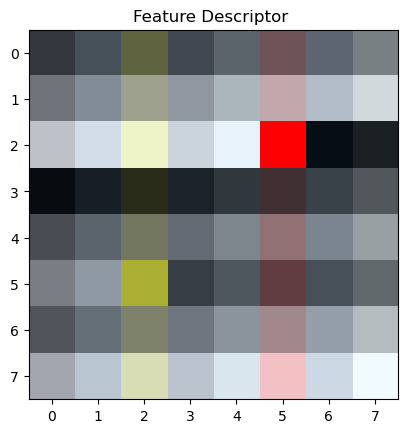
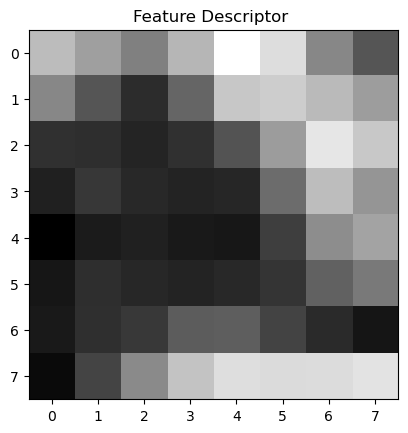
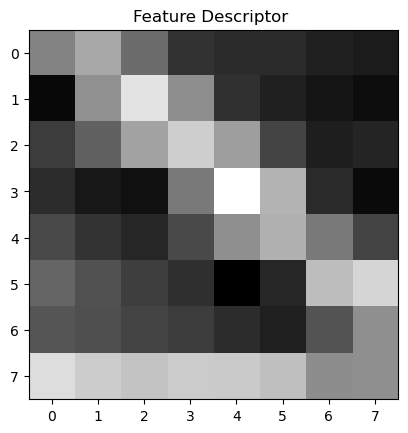
Step 3: Feature Descriptor Extraction

At each of the new points of interest, we can create a patch which describes the feature in that area of the image. Most of the time these are corners, but sometimes these are intersections. By standardizing the feature matrices to be 8x8 from a 40x40 region, we can use correlation algorithms to match these features across images.

I tried both color and black & white features. I found RGB-colored features to work much better than black and white features because the grayscale image reduces information, making the features more similar to each others— which causes issues when we want to match them based on their nearest neighbors.

Feature Regions (40x40) with Red Square (8x8) Feature Matrix

In these images we can see the regions where the 40x40 squares were sample from. In the set below we can also see the upscaled version of those feature vectors!

Step 4: Matching Features

By using methods based on the 1 and 2-Nearest neighbor algorithms, we can match features across two images.
While some of the points match up correctly, the matchings are not perfect. The paper describes an approach which uses Lowe’s Ratio test to prune a significant amount of the false positive matchings.

ALGORITHM: Feature Matching with Lowe's Ratio Test

MATCHING PROCESS:
1. Build KD-Tree:
   Create KD-Tree from fd_X for efficient nearest neighbor search
   Set leaf_size=5 for performance optimization
   Use Euclidean distance metric (Custom Implementation for faster comparisons!)

2. Find Two Nearest Neighbors:
   For each descriptor in fd_2_X:
       Find 2 nearest neighbors in fd_X
       Store distances in nn2_dists
       Store indices in nn2
       
3. Find Single Nearest Neighbor (for additional statistics):
   For each descriptor in fd_2_X:
       Find 1 nearest neighbor in fd_X
       Store distances in nn1_dists
       Store indices in nn1

4. Calculate Threshold Values:
   thresholds = first_nearest_distance / second_nearest_distance
   thresh = mean(thresholds)
   outlier_dist = mean(second_nearest_distances)

5. Apply Lowe's Ratio Test:
   For each descriptor i in fd_2:
       Get distances d1, d2 to two nearest neighbors
       IF d1 < thresh * d2 AND d1 < outlier_dist:
           Add match: [index_in_fd_2, index_in_fd]
OUTPUT:
- Array of matches, where each individual row contains [index in fd_2, corresponding matching index in fd]

We see that only some of the points match up correctly. However, this will be fixed with RANSAC!

Step 5: Robust Matching: RANSAC

In order to find the optimal homography, we can create all possible samples of homography points. However, this number can grow quite high when dealing with scenes with many edges because we would have to effectiveley use $\binom{n}{4}$ differetn combinations for which we would generate homographies, count outliers within our selected $\varepsilon$ radius of inliers, count them and do this. For 40 points, this is just 91390 samples. which is not that bad with modern CPUs. However, 500 points would lead to 2573031125 samples to assess! That will cost a lot of time and energy. So, we rely on the high likelihood that we have various matching correspondence points and run a set number of random samples, hoping to draw a random sample which will contain valid and correct correspondence points. We will know that we found the optimal Homogrpahy because it will have the highest number of inliers!

RANSAC loop:
For i = 1 to num_samples:
  a. Randomly sample points:
      - Select random_subset of size 4 from correspondences
      - Get matching points from both images (c1_sample, c2_sample)
  
  b. Compute homography:
      H = compute_homography(c1_sample, c2_sample)
  
  c. Test homography on all points:
      # Transform all points using H
      warped_points = H × corr_1_ext
      normalize_homogeneous_coordinates(warped_points)
      
      # Calculate errors
      distances = euclidean_distance(warped_points, corr_2)
      
      # Count inliers (points with error < eps)
      inliers = points where distance < eps
      inlier_count = number of inliers
      inlier_error = sum of inlier distances
  
  d. Update best result:
      If (inlier_count > max_inliers) OR 
         (inlier_count == max_inliers AND inlier_error < max_inlier_error * 0.5):
          max_inliers = inlier_count
          max_inlier_error = inlier_error
          H_optimal = H
          Save corresponding points

My implementation of RANSAC takes into account images where inliers could be misleading and uses an added improvement metric to prevent us from using a suboptimal homography which may be encountered early on.

Optimization Criteria:

• Primarily maximizes number of inliers

• Secondary criterion: minimizes total inlier error

• Uses 0.5 factor for error comparison to ensure significant improvement

Mosaic 1

Manually Stitched with 6 Correspondence Points

Auto-stitched with ANMS + RANSAC

Mosaic 2

Manually Stitched with 6 Correspondence Points

Mosaic 3

Manually Stitched with 6 Correspondence Points

Auto-stitched with ANMS + RANSAC

Auto-stitched with ANMS + RANSAC

Mosaic 4: Total Mosaic for House Data Set

Manually Stitched with 6 Correspondence Points

Auto-stitched with ANMS + RANSAC

Sunset Dataset

These images were taken on the wonderful sunset from the Panoramic Apartments in Berkeley, CA. With the sun setting earlier, these Fall nights offer vibrant and captivating data.

Mosaic 5

Manually Stitched with 8 Correspondence Points

Mosaic 6

Auto-stitched with ANMS + RANSAC

Manually Stitched with 8 Correspondence Points

Auto-stitched with ANMS + RANSAC

Mosaic 7: Total Mosaic of Sunset Images 1, 2, and 3

Manual Alignment with Correspondences

Auto-stitched with ANMS + RANSAC

What Have You Learned?

The coolest thing I learned is how powerful linear algebra can really be. Sometimes we think of resorting to ML/deep learning to solve a lot of issues in computer vision, but sometimes it is best to approach things with a simple approach. I was surprised to see how well nearest neighbors performed at matching, combined wit RANSAC, this gave great results. I also doubted that RANSAC would work as well as it does, but even running batches which are a fraction of the size of the total number of combinations, I got amazing results. I also learned a lot from the research paper! Looking forward to reading it again and understanding the parts which we did not implement for this project.